Query Optimization by using Deep Q-learning
Introduction
Join order enumeration has been studied decades, in Postgresql, Dynamic Programming based on left deep was adopted for small queries, while Genetic Algorithm for large queries, both methods are costly and have no optimal guarantee. Q-learning is essentially a Dynamic Programming enumeration method for Markov Decision Process (MDP), it can determine next actions based on the minimum values in Q-table. According to the Bellman Equation, the q-value can be updated as following:
\(\alpha\) is the learning rate, \(\gamma\) is the discount factor.
However, Q-larning based on Q-table is still costly, we can not get the optimal trajectory for each
query online, therefore, we replaced Q-table by a Deep Neural Network Like LSTM in our work.
Deep Q-learning has the ability of generalization, we can train the model on test queries,and the model
can determine the join order of unknown queries faster and better than traditional query optimizer.
In this blog, we first propose a effective Q-learning methed to find optimal join order for single query, and then
we generalize this method to multiple queries, we propose an Inverse Q-Learning method to help the model converge faster
single query and use transfer learning to help the model to determine the join order for unknown queries.
Q-learning for single query
Input Features
For single query, action is the chosen join condition, and the sequence of picked join conditions is enough to depict the state, each action is represented as a one-hot vector where each bit represents whether a join condition was picked. Sequence of selected actions is input to the model as State, and the output is values for different actions.
Model
Because the future cost is also influenced by the order of history actions and RNN model can learn the order features of one sequence, we take LSTM as deep Q-network, the input dimention is the number of join conditions in total and the input length is the number of chosen actions before current state, which contains two hidden layers and one fully connected linear layer as outputs.
Deep Q-learning
We adopt the memory-based Q-learning method with \(\epsilon\) gradient, we optimize the query many times. In one episode, we select next actions according to the output of LSTM for current state greedily until all the join conditions have been selected. In order to explore more policies at begining, we have chance to randomly select actions, but the chance would decrease exponentially for convergence. Each time we select an action and step into next action, the tuple \((S,a,S',R)\) would be stored into memory and the model will be updated once according to the sampled memories. We have many options for reward function. Here we choose logarithm of total cost of the query as the reward of terminated state and zero for other states. According to the Bellman Equation, the reward would be back propagated to every state in the end.
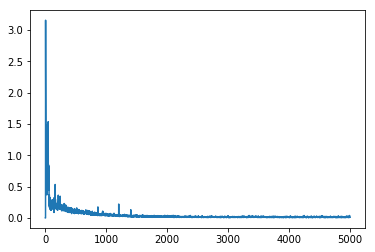
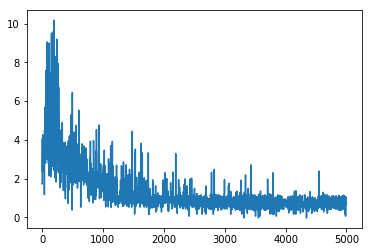
Results
As Figure below shows, our method for single query can converge within 1,000 episodes, loss convergence means that the model knows
the true value of each seen policy while the reward would takes more episodes to converge to the optimal cost, around 2,500 episodes.